The Polymorphic Cipher - not too technical
 Download this paper as PDF document
Download this paper as PDF document
 The history of cryptography has shown that unbreakable ciphers had in many cases been cracked shortly after their widespread use had begun. One famous example is the "Enigma" encryption machine used by the Nazis in world war two: British specialists at Bletchley Park had been able to crack the clever permutation code. This resulted in detailed knowledge about most German military operations and in the total loss of the German submarines.
The history of cryptography has shown that unbreakable ciphers had in many cases been cracked shortly after their widespread use had begun. One famous example is the "Enigma" encryption machine used by the Nazis in world war two: British specialists at Bletchley Park had been able to crack the clever permutation code. This resulted in detailed knowledge about most German military operations and in the total loss of the German submarines.
The widespread DES algorithm has long been supposed to be unbreakable. In January 1999 a test performed by RSA Data Security, Inc. (San Mateo, Calif., USA) proved that it takes less than 22.25 hours to crack the 56 bit algorithm by brute-force (by trying all 256 possibilities). That was 365 days after the same company needed 41 days for that task! RSA claim to have a much better cipher, which is obviously true.
Today a code length of 128 bit is regarded as safe by experts (1000 bit for RSA). Thus, it took just 25 years for the experts to actually double their requirements in key size (which is effectively 10000000000000000000 times more than what was initially regarded as "safe"!!!).
Technology advances quickly. Day by day it becomes more likely that somebody is able to decrypt files containing confidential data. Why not simply oversize and make the encryption algorithm variable to solve this nasty but inevitable security problem?
To make the encryption algorithm variable is a new idea - ours. And long keys are usually claimed to slow down the algorithm too much. That's true because execution time increases at least by the key size at the power of two.
A new approach implying self-compiling machine code solves those problems and opens the doors to a new era. Execution time increases only linearly with key size. The idea behind it is to make the algorithm itself a variable. That’s why I have named it „Polymorphic Method“.
What if both data and the actual encryption algorithm are undefined in the beginning. An Opponent who wants to break your key feels deprived of any constant. Working with variables only quickly becomes pretty complex.
Commonly known ciphers use one key - say one variable only. An attacker can either try to find a weakness in the design of the cipher or he can try each key.
Polymorphic Ciphers add another dimension - the actual encryption algorithm is determined by the key. An attacker can either try to find a weakness in the design of each and every cipher, the crypto compiler or he can try each key.
The Polymorphic Cipher is among the strongest ciphers available today and it's probably the strongest. The method simply takes advantage of machine code assembled in a way that almost appears to be random to yield extraordinary security against all kinds of attacks. It is even intrinsically safe against the analysis of the program's instruction sequence because the instruction sequence itself is a variable! It is important to know that the key assumption for successful cryptoanalysis is detailed knowledge of the encryption algorithm - but the actual Polymorphic Method’s algorithm is inherently UNKNOWN.
Basic principle of a theoretical Polymorphic Cipher Method
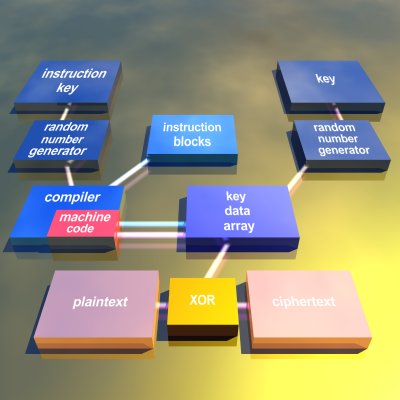 Two different passwords (or two parts of one password) are compressed by a hash algorithm. One part of the hash is used to compiled machine code of the actual encryption algorithm. The compiler simply assembles standardized building blocks, adjusts addresses as well as entry- and exit points to generate a piece of machine code which affects the key data array (internal state) during execution of the machine code. The key data array is initialized by the remaining part of the hash.
Two different passwords (or two parts of one password) are compressed by a hash algorithm. One part of the hash is used to compiled machine code of the actual encryption algorithm. The compiler simply assembles standardized building blocks, adjusts addresses as well as entry- and exit points to generate a piece of machine code which affects the key data array (internal state) during execution of the machine code. The key data array is initialized by the remaining part of the hash.
After the machine code has been executed, a small part of the content of the key data array (internal state) can be used to encrypt plaintext through the application of the xor function. XORing the internal state is dangerous as this simple function exposes information that should be kept secret. A practical Polymorphic Cipher will always use the content of the key data array to bias an underlying cryptographic algorithm which is simple and fast. By doing this, the complexity of the secrecy system increases as it’s more difficult to analyze the internal state of the key data array, although the information it contains does not expose the key nor does it enable for cracking the cipher.
It is even more confusing to sometimes recompile the instruction sequence. This makes the method dynamically polymorphic.
The compiler internal to the Polymorphic Encryption Method compiles interchangeable code fragments which use the processor’s registers in an identical way. Each building block can be exchanged by any other. The actual code length can vary due to differences in complexity but not the way data is passed from one building block to the other. A data array is used as a long variable which is initialized by part of compressed password. It takes the place of the internal state as known from conventional ciphers. The CPU works on this key data array and performs permutations, modulo-divisions, shifts and other nonlinear operations.
An implementation of a Polymorphic Method is publically available as a Windows software called „TurboCrypt“. It’s crypto engine uses the CPU register ebx as input and output register, eax as general purpose buffer and ebp as base pointer to the key data array. The key data array that ebp points at is 512 bit long.
Example of a simple building block
The xor operation alters ebx and four bytes of the key data array:
push ebp; // save the start address of the key data array for later
mov eax,123; // load offset: constant data which was calculated by the compiler
add ebp,eax;
mov eax,[ebp+0];// load internal_state[ebp+0] in AL and internal_state[ebp+1] into
// next upper byte of eax and so on up to internal_state [ebp+3]
xor ebx,eax; // this instruction can be replaced by another or a set of instructions
xor [ebp+x],ebx;// change the key data array frequently; x is defined by the compiler and
// chooses one element of the key
pop ebp; // restore start address of the key data array
Instead of simply using an xor function, it is of course possible to calculate sums, to perform shifts, multiplications and modulo divisions, as well as to calculate pseudorandom numbers with more complex instruction combinations. A good implementation of the presented method will rely on a set of building blocks which change a large part of the internal state and not just 32 bit. Simple xor instructions, as well as addition and subtraction are cryptographically weak (actually by far more than extremely weak), but the general code assembly methodology can easily be demonstrated with them.
An example for a much more cryptographically safe building block is a CRC32 implementation:
The function calculates a 32 bit CRC according to IEEE 802. The polynomial is: x32 + x26 + x23 + x22 + x16 + x12 + x11 + x10 + x8 + x7 + x5 + x4 + x2 +x + 1. X32 does of course not exist and the 1 only inverts the input data. Thus, the polynomial can be written as: $04C11DB7
push ebp; // ebp MUST never be really destroyed
and eax,127; // perform an operation with four key bytes at a
//time using eax from the previous instruction block
add ebp,eax;
mov eax,[ebp+0]; // load internal_state[ebp+0] in AL and internal_state[ebp+1] in
// the next upper byte of eax and so on up to internal_state[ebp+3]
mov esi,ebp; // save ebp for later to alter the key
pop ebp; // get original base of the key data array
push ebp; // restore stack frame
push ebx; // save ebx for later
mov ecx,32; // counter for the loop
xor edx,edx; // edx is used to clear the zero flag before the loop @rep1 command below
@rep1:rcl ebx,1; // shift data in from ebx
rcl eax,1; // use eax as CRC buffer
jnc @cnt1; // CRC decision
xor eax,$04C11DB7; // xor with IEEE 802 generator polynomial
@cnt1:add dl,1; // clear Zero-Flag (will be rarely necessary)
loop @rep1;
pop ebx; // restore old ebx value. ebx keeps a running 32 bit result
mov ebp,esi; // get the address of the previously selected bytes of the internal_state
mov [ebp+0],eax; // alter the internal_state
xor ebx,eax; // alter ebx
// here is the end of the CRC routine
pop ebp; // exit the routine by restoring the original ebp
The presented building block only affects four bytes of the internal state. Depending on the size of the key data array (internal state) it should affect much more data for good attack security. It is very simple to extend the routine to satisfying this necessity.
It is possible to add loops over one or more instruction blocks. This is usually performed by adding the 80386 loopne-command. The algorithm thus spends more time on crunching instructions. By altering ebp with every loop cycle, the internal state can influence the algorithm. This way an interdependence between internal state and actual encryption algorithm is created.
The very first implementation of such a Polymorphic Cipher compiled an 8192 bit password and was still pretty fast. This method enables for an unprecedented flexibility. Any practical key size and any practical size of the compiled algorithm can be obtained.
There is no reason to condemn ciphers with more than 256 bit keyspace, especially not a Polymorphic Cipher.
Why that?
The answer is simple: If Brute Force is the only way to attack a cipher, it’s a big disadvantage for an attacker if one instance of the cipher to be cracked has a very small footprint on a silicon wafer.
Why?
Because a Brute Force Attack relies on millions of instances running in parallel. AES is thus very well suitable to apply Brute Force as the algorithm can be implemented on a tiny piece of silicon.
Attack security
Besides the classical features as a secrecy system, notably mapping plaintext into ciphertext by applying a one-way function with an internal state that is initialized with the key, Polymorphic Ciphers are highly variable.
If there are only 4 cryptographic instruction blocks or building blocks (this could be AES Rijndael, AES Twofish, Magenta and Mars) and 16 of these blocks can be assembled chaotically one after the other, there exist 416 = 4294967296 different possibilities for the actual encryption algorithm! If 128 instruction blocks were to be assembled, a choice of 4128 = 1,158*1077 combinations would result (standard 128 bit encryption yields a total of 3,403*1038).
The Polymorphic Method features a substancially higher attack security than any conventional method. In order to calculate the total attack security, the number of code combinations must be multiplied by the number of combinations of the internal state . Key size may be 16 bytes = 128 bits; thus there exist 2128 = 3,403*1038 key combinations in the classical sense (of the internal state). The two keyspaces multiplied yield 1,158*1077 * 3,403*1038 = 3,913*10115 possible key combinations for a Polymorphic Cipher with 128 bit internal state and 4128 = 1,158*1077 code combinations.
In order to compare conventional cryptographic methods with the Polymorphic Method, the total keyspaces must be compared. As both methods are assumed to work on a 128 bit internal state (like AES Rijndael), this comparison is legal. Thus, the polymorphic method beats any conventional method by a factor of 3,913*10115 / 3,403*1038 = 1,150*1077 (!). This is more than the number of atoms on our planet!
The actual implementation in the cryptographic program „Best Possible Privacy“, which had more than 20.000 users in the year 2000 and 2001, used 32 instructions and three bit of constant data per instruction. Thus, there were 32 ways to affect the algorithm multiplied by 8 possibilities for constant data => 256 = 28 variations
The algorithm was limited to 1024 instruction blocks. Thus there were 2(1024 * 8) = 28192 different code combinations possible and equally probable! The 256 byte internal state further enhanced attack security to yield 28192 * 22048 = 210240. Note that nearly 100% of the security stems from the actual cryptographic algorithm being totally variable.. The new method uses commonly known techniques but enhances them significantly.
Attacks and their likelyhood of success on the Polymorphic Method
Attacks are not algorithms, but instead just general approaches which must be reinvented for every new type of cipher.
It is generally assumed that the Opponent knows the design of the cipher and has virtually any amount of plaintext and corresponding ciphertext ("known plaintext"). It is further assumed that The Opponent has the real-time ability to obtain "defined plaintext" by enciphering messages at will and collecting the resulting ciphertext.
Exhaustive Search (Brute Force on the keys)
Try each possible key until the message deciphers properly. Try most-likely keys first.
A keyspace of at least 128 bits should be sufficient to prevent exhaustive search in the foreseeable future. The keying system for the Polymorphic Method is hard to implement with less than 256 bits and has usually a keyspace substancially beyond this value – 512, 2048, 8192 bit or more, not counting the key combinations for the instruction key which usually provide more than 99.9999999999% of the total security.
A very important aspect of Polymorphic Encryption is a feature that might be regarded as a disadvantage:
Practical ciphers consume a lot of chipspace. For a PC application this is no problem, although PMC requiring 100 or 1000 times more memory resources and a powerful microprocessor. PMC on a smartcard although is a challenge to implement.
The advantage although is that key setup time is hundreds of times slower with PMC compared with DES, AES or other classical symmetric algorithms. An attacker requires hundreds of times more resources to try and find the right key bit pattern.
Chosen Key
Try various keys on known plaintext and compare the resulting ciphertext to the actual ciphertext, to try and build the correct key value.
As the key is more or less the algorithm itself, the task of an opponent is hopeless because the one-way polymorphic function comes in different shapes for each and every key bit pattern. As the keyspace is rather big, there is no possibility to isolate and work separately on some kind of table. A computer can theoretically only be as big as there are atoms on this planet.
Ciphertext-Only Codebook
Collect as many ciphertexts as possible and try to understand their contents through usage and relationships; then, when a ciphertext occurs, look it up. This treats the block cipher like a code, and is the classic approach to code-breaking.
Just as some letters are more frequently used than others, words and phrases also have usage frequencies, as do blocks which contain plaintext. If the internal state size is small (under 64 bytes), and if the ciphering key is not changed frequently, it may be possible to build a codebook of block values with their intended meanings.
Codebook attacks of any sort are ideally prevented by having a large number of block values, which implies a large size for the internal state. Once the block size is at least, say, 64 bytes, it can be expected that the amount of uniqueness in each block exceeds anyone's ability to collect and form a codebook. This was the main weakness of DES and AES is likely to feature the same deficiency.
Since the complexity of any sort of a codebook attack is related to block size only, doing "triple" anything will not affect increase this complexity. In particular, this means that Triple DES is no stronger than DES itself under this sort of attack, which is based on block size and not transformation complexity.
The Polymorphic Method is best implemented with a 512 bit … 8192 bit block size and the instruction sequence changing with every block. The method is further ideal for producing a seed for some random number generator which decouples the algorithm from the generation of the confusion sequence. Because a Polymorphic Method comes in different shapes with each key, any kind of codebook will contain mostly noise and will not be of great use.
Known Plaintext
Somehow "obtain" both the plaintext and the corresponding ciphertext for some large number of encipherings under one key.
With this kind of attack, one plaintext-ciphertext pair contains sufficient information to obtain the content of the internal state. In order to identify a key, both subkeys (compiler subkey and the subkey for the internal state) must be guessed using the Exhaustive Search method.
As both the input to the compiler as well as the subkey for the internal state are unknown, it is difficult to reveal the full internal state without revealing the underlying crypto system. The Polymorphic Method hides between 25 to 75% of subkey information in the actual instruction code and that alone provides more than sufficient complexity. Note that a single known plaintext and ciphertext pair probably would identify a DES key!
Known-Plaintext Codebook
Collect as many ciphertexts and associated plaintext blocks as possible; then, when a ciphertext occurs, look it up.
When using small block ciphers codebook attacks can be prevented by randomizing the plaintext (often using Cipher Block Chaining) so that the plaintext block values are distributed evenly across all possible block values.
Codebook attacks are although ideally prevented by having a large number of block values, which implies a large block size. To prevent this attack for the future, a block size of 256 bit is regarded as safe so the uniqueness it does contain assures that there will be too many different blocks to catalog.
As the key is more or less the algorithm itself, the idea to create a table ends in logging noise when this kind of attack is excercised on a Polymorphic Cipher.
Chosen Plaintext
Without knowing the key, arrange to cipher data at will and capture the associated ciphertext. Dynamically modify the data to reveal the key, or keyed values in the cipher.
The point here is not to decipher the associated ciphertext because the opponent is producing the original plaintext. If an opponent has chosen plaintext capabilities, he can probably also submit arbitrary ciphertext blocks for deciphering.
The weakness to be exploited here usually depends upon the ciphering system beyond the core cipher per se - a point with little internal state. As far as the Polymorphic Method is concerned, there is no static algorithm with some known weakness. Instead, there are a lot of possible weaknesses – for each possible keyed state. As a matter of consequence, the Chosen Plaintext attack is not applicable here.
DES or AES are static algorithms. A Chosen Plaintext attack might be yield good results if applied on such ciphers.
Chosen-Plaintext Codebook
Create as many ciphertexts and associated plaintext blocks as possible; then, when a ciphertext occurs, look it up.
This is much like the previous codebook attacks, now with the ability to fill the codebook at will and at electronic speeds. Again, the ability to do this depends upon the cipher having a relatively small block size and a static cryptographic algorithm would be a good target.
This attack is again unpractical to apply on a Polymorphic Cipher because it’s simpler and more efficient to try all possible keys than to store codebooks for each and avery combination of base ciphers.
Meet-in-the-Middle
With a multi-layered structure, given known-or defined-plaintext, search the top keyspace to find every possible result, and search the bottom keyspace to find every possible value.
With a two-level construct and a small block size, matches can be verified with a few subsequent known-plaintext/ciphertext pairs. Of course, three and more-level constructs can always be partitioned into two sections so a meet-in-the-middle attack can always be applied; this just may be pretty complex.
As each layer in a good crypto algorithm contains a huge amount of keyed state or „keyspace“, the Polymorphic Method uses a large key and consequently adds a huge amount of unknown algorithm which renders this kind of attack useless as it requires the cipher that is attacked to be static.
Key Bit Bias
Through extensive ciphering of fixed plaintext data under a variety of different keys, it may sometimes be possible to associate key bits with the statistical value of some ciphertext bits. This knowledge will break a conventional cipher quickly.
As different keys inevitably produce different cipher algorithms, statistics cannot help to link ciphertext with plaintext when attacking a Polymorphic Cipher. There’s simply a new independent variable in the game with the Polymorphic Method as each key state has some pretty unique weakness and not a constant one which is required for this attack to be successful.
Differential Cryptanalysis
Exploit known properties of particular known substitution tables to effectively reduce the number of "rounds" in an iterated block cipher.
The original form of Differential Cryptanalysis mainly applies to iterated block ciphers with known tables, neither of which are present in Polymorphic Encryption Algorithms. For an iterative cipher like DES, statistical unbalance can be found in known, fixed substitutions and this can be exploited to peer back into previous iteration steps.
For the Polymorphic Cipher Method, each different input value will actually select a different cipher, and this results in a completely variable transformation. It is hard and very inefficient to attack a transformation which changes its structure completely whenever it is probed.
Summary
Except for the possibility to gain knowledge of the final state of the key data array which holds the internal state) in a basic Polymorphic Cipher Configuration using XOR as combiner, there is nothing else to find out. There is no possibility to identify a key other than by searching exhaustively (Brute Force Attack). The available keyspace is much greater than for any other cryptographic method. In order to compare the presented method with conventional methods, a conventional method has some data keyspace and only one possibility for the algorithm. The presented Polymorphic Method features as well a data keyspace, but is complemented by an additional algorithm keyspace. All in all, the new method features a dramatic increase in security compared to common approaches.
It is worth imagining that cryptographically strong ciphers like DES, GOST, IDEA; Hashes, etc. may be the set of building blocks of the Polymorphic Cipher. Weaknesses of each specific building block would vanish. The result would probably be a perfect cipher.
Speed
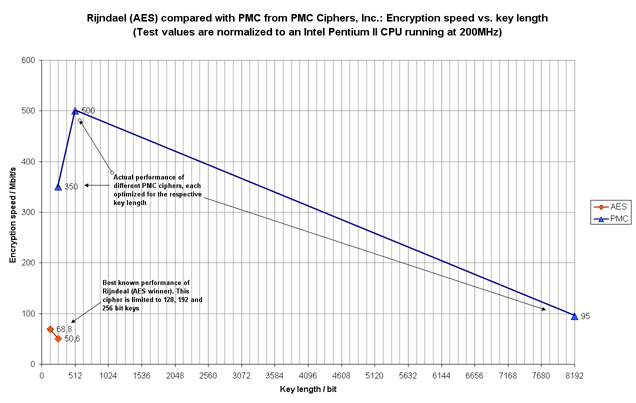
The original implementation of PMC in the BPP file encryption tool is by far too slow when compared with the latest developments.
The latest variant with 512 bit key length is implemented in PMC Ciphers TurboCrypt. This crypto engine comes with an encryption speed of 500Mbit/s, which is approximately 10 times the speed of AES (Rijndael algorithm) operating with 256 bit keys!
TurboCrypt is a hard disk encryption tool which adds encrypted file-hosted volumes. It is available for Microsoft Windows operating systems.
Conclusion
For PMC, which was secret of state in 1999 in Germany, there exists no attack other than exhaustive search which is applicable on any cipher. There’s no theoretical or practical way to reconstruct keys from plaintext.
The presented method comes with a comparable „data keyspace“ as conventional symmetric encryption methods. It adds a significant amount of possible and equally probable algorithmic keys, thus yielding substancially higher security and speed.
This is a preliminary document and may be changed substantially prior to final commercial release. This document is provided for informational purposes only and PMC Ciphers makes no warranties, either express or implied, in this document. Information in this document is subject to change without notice. The entire risk of the use or the results of the use of this document remains with the user. The example companies, organizations, products, people and events depicted herein are fictitious. No association with any real company, organization, product, person or event is intended or should be inferred. Complying with all applicable copyright laws is the responsibility of the user. Without limiting the rights under copyright, no part of this document may be reproduced, stored in or introduced into a retrieval system, or transmitted in any form or by any means (electronic, mechanical, photocopying, recording, or otherwise), or for any purpose, without the express written permission of PMC Ciphers.
PMC Ciphers may have patents, patent applications, trademarks, copyrights, or other intellectual property rights covering subject matter in this document. Except as expressly provided in any written license agreement from PMC Ciphers, the furnishing of this document does not give you any license to these patents, trademarks, copyrights, or other intellectual property.
© 2001 – 2002 ciphers.de, © 2002-2008 PMC Ciphers, Inc. & © 2007-2008 Global IP Telecommunications, Ltd All rights reserved.
Microsoft, the Office logo, Outlook, Windows, Windows NT, Windows 2000, Windows XP and Windows Vista are either registered trademarks or trademarks of Microsoft Corporation in the U.S.A. and/or other countries.
Company and product names mentioned herein may be the trademarks of their respective owners.